Die dynamischen Arrayfunktionen von Excel aus Microsoft 365 ermöglichen Vieles, was in der Vergangenheit nur umständlich oder auch gar nicht per Formel umsetzbar war.
Im heutigen Artikel werden ein paar dieser Funktionen kombiniert, um sehr elegant zufällige Zahlenreihen zu generieren. Ich möchte es aber nicht bei einem akademischen Selbstzweck belassen, sondern gleich noch ein paar Anregungen für einen möglichen Praxiseinsatz aufzeigen, die vielleicht auch für dich interessant sein könnten.
Die Idee zu diesem Artikel entstand aus einem kleinen LinkedIn-Beitrag von Global Excel Summit, über den ich vor einiger Zeit gestolpert bin. Dort wurde gezeigt, wie man zufällige Zahlenreihen (ohne Wiederholung) generiert. Ruhm und Ehre gebührt also voll und ganz dem Global Excel Summit.
Es gibt ja in Excel verschiedene Zufallsfunktionen. Das sind die alten Bekannten ZUFALLSZAHL und ZUFALLSBEREICH, in Microsoft 365 ist dann noch die wesentlich flexiblere ZUFALLSMATRIX dazugekommen.
Diese Funktionen generieren mehr oder weniger zufällige Zahlen, haben aber alle den Nachteil, dass es dabei zu Wiederholungen kommen kann, wenn man Zahlenreihen damit generiert. Das ist in manchen Fällen auch kein Problem, in einigen Szenarien aber doch unerwünscht. Aber zum Glück gibt es dafür Lösungen.
Fall 1: Zahlenreihe ohne Wiederholung
Im ersten Beispiel wird einfach eine zufällige Zahlenreihe generiert, die keine Wiederholungen enthält. Das heißt, jede Zahl kommt nur ein einziges Mal vor.
Drei Funktionen werden dazu kombiniert:
SEQUENZ
ZUFALLSMATRIX
SORTIERENNACH
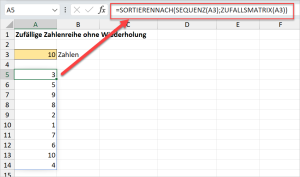
Um das Ganze etwas flexibel zu gestalten, wird die Anzahl der gewünschten Zahlen über eine Eingabezelle bestimmt (A3). In Zelle A5 steht dann die folgende Formel:
=SORTIERENNACH(SEQUENZ(A3);ZUFALLSMATRIX(A3))
Genau genommen ist dabei nicht die Zahlenreihe an sich zufällig, sondern nur die Sortierung. Da es sich um dynamische Arrayfunktionen handelt, dehnt sich der Ausgabebereich abhängig von der angegebenen Zahl in A3 auch dynamisch aus. Wie funktioniert diese Formel jetzt genau?
Die SEQUENZ-Funktion erzeugt einfach eine Reihe an Zahlen. Da wir als einziges Argument nur den Wert aus A3 übergeben, wird eine fortlaufende Liste aus ganzen Zahlen produziert, beginnend ab dem Wert 1.
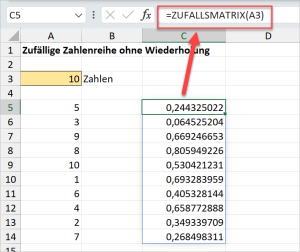
Die Funktion ZUFALLSMATRIX generiert in unserem Beispiel Zufallszahlen im Bereich zwischen 0 und 1. Als eigenständige Formel würde dabei etwas wie in Bild 2 herauskommen:
Drückt man nun wiederholt die F9-Taste, werden die Zufallszahlen neu generiert. Diese Zufallszahlen werden dann die Basis für die Sortierung der Zahlenfolge aus der SEQUENZ-Funktion.
Bleibt noch die Funktion SORTIERENNACH, mit der man eine Liste sortieren kann. Anders als die SORTIEREN-Funktion erwartet sie aber nicht zwingend eine Spalte, nach der sortiert wird. Stattdessen kann man eine andere Matrix als Sortierkriterium angeben. In unserem Fall wäre das eben die ZUFALLSMATRIX.
Ein relativ simples Beispiel, bei dem, wie schon erwähnt, eigentlich nur die Sortierreihenfolge zufällig ist. Die Zahlenreihe an sich enthält nur die ganzen Zahlen beginnend ab 1.
Fall 2: Zufällige Zahlen aus einer Gesamtmenge auswählen
Etwas anspruchsvoller ist dieses Szenario, an das sich vielleicht noch einige aus dem Stochastik-Unterricht erinnern: Ziehe aus einer Schale mit x Murmeln eine Menge von y Murmeln ohne Zurücklegen. Oder besser bekannt durch das Lottospiel 6 aus 49.
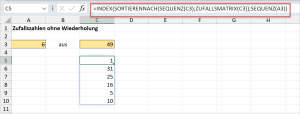
Diese Aufgabe lässt sich mit folgender Formel lösen:
=INDEX(SORTIERENNACH(SEQUENZ(C3);ZUFALLSMATRIX(C3));SEQUENZ(A3))
Dröseln wir die Formel zum besseren Verständnis wieder in ihre Bestandteile auf. Der größte Teil davon entspricht genau dem, was wir schon im vorherigen Beispiel gesehen haben:
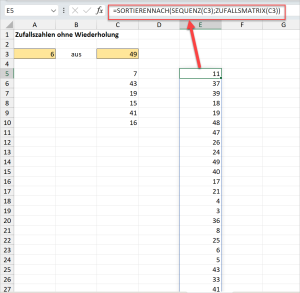
SORTIERENNACH(SEQUENZ(C3);ZUFALLSMATRIX(C3))
Hier wird einfach wieder eine zufällig sortierte Zahlenreihe generiert, die den Wert aus Zelle C3 als einzige Parameter benötigt. Für das Beispiel 6 aus 49 ergibt das also eine Zahlenreihe von 1 bis 49, nur eben zufällig sortiert.
Die umschließende INDEX-Funktion greift auf diese zufällig sortierte Reihe zu und holt sich daraus die ersten 6 Werte.
=INDEX(Zufällig_sortierte_Zahlenreihe;SEQUENZ(A3))
Die INDEX-Funktion würde normalerweise immer nur einen einzigen Wert zurückliefern. Da wir aber für den zweiten Parameter die SEQUENZ-Funktion nutzen, wird ein dynamischer Ausgabebereich erzeugt. Diese SEQUENZ-Funktion generiert einfach eine fortlaufende Zahlenreihe, die bei 1 beginnt und bei dem Wert aus Zelle A3 endet. Im Beispiel also die Zahlen 1 bis 6.
Und damit steht der nächsten Ziehung der Lottozahlen nichts mehr im Wege!
Welche weiteren praktischen Anwendungsfälle sind damit denkbar?
Anwendung: Prüfungsgenerator
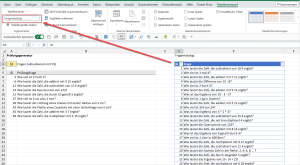
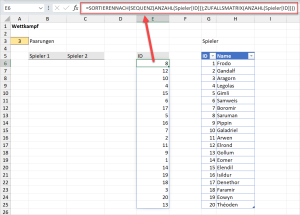
Nehmen wir an, du bist Lehrer und hast dir im Laufe der Jahre einen langen Katalog an Prüfungsfragen zusammengetragen. Warum das Rad immer neu erfinden, man kann ja auf Bewährtes zurückgreifen und sich aus diesem Katalog beispielsweise 10 (20, 30) zufällige Fragen auswählen lassen. Etwa so, wie im folgenden Bild:
Rechts gibt es eine formatierte Tabelle mit den Namen „Fragenkatalog“, über die Eingabezelle A3 wird die Anzahl der zufälligen Fragen festgelegt, die dann in der Liste darunter automatisch ausgegeben werden.
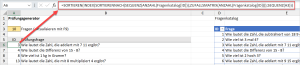
Wir benötigen für die Lösung zwei Formeln. In Zelle A6 verwenden wir im Kern die schon bekannte „Lotto-Formel“ aus dem vorhergehenden Beispiel. Es gibt nur zwei kleine Besonderheiten:
Damit man auch besser erkennen kann, dass wirklich auch keine Frage mehrmals vorkommt, ist die Ausgabeliste nach der Frage-ID sortiert. Dazu wird die Formel einfach noch um eine umschließende SORTIEREN-Funktion erweitert.
Und damit in Zukunft auch neue Fragen berücksichtigt werden können, wird die Anzahl der vorhandenen Fragen im Fragenkatalog jeweils dynamisch mit der ANZAHL-Funktion berechnet.
Das ganze Konstrukt sieht dann so aus:
=SORTIEREN(INDEX(SORTIERENNACH(SEQUENZ(ANZAHL(Fragenkatalog[ID]));ZUFALLSMATRIX(ANZAHL(Fragenkatalog[ID])));SEQUENZ(A3)))
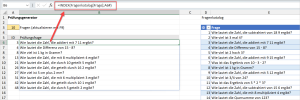
Und ab Zelle B6 wird nun über die INDEX-Funktion die zur ID gehörende Frage aus dem Katalog angezeigt:
=INDEX(Fragenkatalog[Frage];A6#)
Das #-Zeichen in A6# bedeutet, dass auf das dynamische Array in Zelle A6 zugegriffen wird. Das bedeutet, dass sich auch die INDEX-Zeilen immer an die Anzahl der IDs in Spalte A anpassen.
Anwendung: Turnier-Gegner auslosen
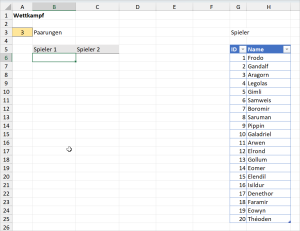
Ein weiterer Anwendungsfall könnte im sportlichen Bereich liegen. Wie etwa die Zulosung von zwei Wettkampfgegnern oder Paaren in einem Turnier. Für meine Beispiel habe ich in Spalten H:I eine formatierte Tabelle mit allen Spielern meines Turniers angelegt. Nun sollen aus dieser Tabelle immer zwei Spieler gegeneinander antreten, die Anzahl der zu bildenden Paare wird in Zelle A3 festgelegt.
Natürlich ist es auch hier wichtig, dass jeder Spieler nur in einer einzigen Paarung vorkommen darf. Diesmal gehen wir jedoch ein bisschen anders vor und erstellen zunächst eine zufällig sortierte Tabelle mit den IDs aller Spieler:
=SORTIERENNACH(SEQUENZ(ANZAHL(Spieler[ID]));ZUFALLSMATRIX(ANZAHL(Spieler[ID])))
Soweit nichts Neues.
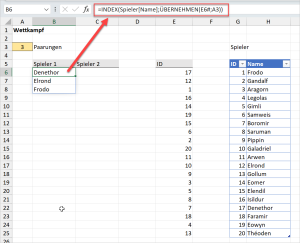
Nun kommt die Formel für die Spieler 1. Dafür brauchen wir aus unserer zufällig sortierten ID-Liste nur so viele IDs, wie es Paarungen gibt. Damit alles schön dynamisch bleibt, verwende ich dafür die ÜBERNEHMEN-Funktion, die ich kürzlich in diesem Artikel vorgestellt habe. Damit lassen sich aus einer Liste die ersten (oder letzten) Datensätze übernehmen:
=INDEX(Spieler[Name];ÜBERNEHMEN(E6#;A3))
Da es laut Zelle A3 insgesamt 3 Paarungen geben soll, werden durch die ÜBERNEHMEN-Funktion nur die ersten 3 IDs aus der Liste an die INDEX-Funktion geliefert.
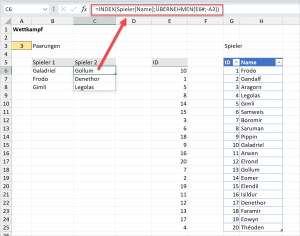
Für die Spieler 2 möchte ich die letzten IDs aus der unsortierten Liste verwenden. Die ÜBERNEHMEN-Funktion erwartet dafür als zweiten Parameter einen negativen Wert, daher das Minuszeichen vor dem Zellenbezug A3:
=INDEX(Spieler[Name];ÜBERNEHMEN(E6#;-A3))
Und schon haben wir eine dynamische Zuteilungen von Wettkämpfern, die bei jedem Drücken der F9-Taste neu generiert wird.
Ich bin sicher, dir fallen sicher noch einige andere Anwendungsfälle ein. Wenn ja, dann lass es uns in den Kommentaren wissen!

P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.







Großartig, doch die paarung Pippin vs. Gandalf fand ich etwas grausam 😉
Hallo Peter,
danke für dein Feedback 🙂
Im Zweifelsfall muss man halt ein paarmal F9 drücken, bis es passt. Und im Zweifelsfall wächst man ja mit seinen Aufgaben…
Schöne Grüße,
Martin
Hallo Martin,
so etwas ähnliches hatte ich bei einer Excel2010-Datei für die Auswertung eines Skat-Turniers mit ca. 50 Teilnehmern und zwei Spielrunden zu 48 Partien. Die erste Runde wurde zugelost (siehe Dein Blog), die zweite Runde nach Ergebnissen der ersten Runde (absteigend) besetzt.
Als Schwierigkeit kommt noch dazu, dass man je nach Teilnehmerzahl unterschiedliche Zahlen von Dreier- und Vierer-Tischen hat (48 Spieler = 12 Vierer-Tische; 50 Spieler = 11 Vierer-Tische und 2 Dreier-Tische).
Mit dem Wechsel von Excel2010 auf Excel2016 hat die Datei auf einmal nicht mehr richtig funktioniert … ich habe versucht sie umzuschreiben und anzupassen, bin aber gescheitert.
Vielleicht ist das ein Anreiz, dass ich mir Excel365 zulege …
Viele Grüße,
Frank
Hallo Frank,
ja, das hört sich nach einer kniffeligen Aufgabe an. Dass es ein Problem beim Wechsel von 2010 auf 2016 gab, klingt allerdings sehr merkwürdig, denn es kamen damit ja nur neue Funktionen dazu.
Was Excel 365 angeht: Das Abo-Modell ist sicherlich nicht jedermanns Fall. Aber aus meiner Erfahrung heraus kann ich nur sagen, dass ich es nicht mehr hergeben möchte, denn insbesondere die ganzen neuen Array-Funktionen machen das Leben so viel leichter…
Schöne Grüße,
Martin
Meine ersten Zufallspaarungen: Gimli gegen Aragorn, Samweis gegen Gandalf, Denethor gegen Galadriel. Nach Peter Jansen nicht das erste Mal, dass Gandalf einen Hobbit schlachten muss 😉
Richtig schöne Anregungen, hat mir viel Freude gemacht und ich hoffe schon richtig darauf, dass sich eine Gelegenheit in meinem Job ergibt, das einzusetzen (Zufallsfunktionen fristen bei mir bislang vorrangig ihr dasein als Hilfsmittel zur Erstellung von Übungsaufgaben für unsere Azubis – im Controlling stellen wir meist echte Gegebenheiten und logische Prognosen auf, da ist der Zufall kein so bedeutendes Element, aber mit ein paar klug gesetzten Parametern lassen sich sicher auch mal Erkenntnisse aus Versuchsmodellen entwickeln)
Ich halte euch auf dem Laufenden, wenn sich was ergibt =)
Hallo Julius,
auweh, die armen Hobbits 🙁
Ja, in der Planung ist der Zufall nicht immer so richtig gefragt, auch wenn die Realität dann doch meistens durch zufällige Ereignisse gesteuert wird…
Schöne Grüße,
Martin
Danke für die lehreichen Ausführungen. Ich hätte jetzt nu r noch eine Frage:
Ich möchte für ein Kartenspiel die Paarungen auslosen und noch auslosen welche Paarung gegen welche Paarung spielt, wobei ich vermeiden möchte, dass 2 oder mehrere Spieler, bei weitern Runden Zusammentreffen. Das Spiel geht über 5-6 Runden mit 40-60 Spielern. Danke im Voraus für die Hilfe.
Hallo Erich,
hier würde sich vermutlich ein zweistufiges Vorgehen anbieten: zuerst werden wie oben beschrieben die Paarungen ermittelt. Und in einer zweiten Stufe wird dann die Liste aller Paarungen als Ausgangsliste für die nächste Stufe verwendet. Hier könnten dann die gleichen Formeln angewendet werden, wie für die erste Stufe.
Schöne Grüße,
Martin
Hallöchen Martin,
kannst du mir erklären, wie ich „6 aus 49“ auch in einer anderen Excel-Version eingeben kann? Ich brauche jeweils 40 zufällige Zahlenreihen mit jeweils 9 Zahlen. Ich möchte ein Spiel zur Hochzeit meines Bruders damit vorbereiten.
SEQUENZ gibt es jedoch in meiner Version nicht,
Viele Grüße
Silke
Hallo Silke,
du müsstest noch erläutern, wie die genauen Anforderungen sein sollen:
Darf jede Zahl über alle 40 Reihen genau nur ein einziges Mal vorkommen?
Oder muss die Zahl nur innerhalb jeweils einer der 40 Reihen eindeutig sein?
In welchem Bereich sollen die Zahlen pro Reihe liegen?
…
Schöne Grüße,
Martin
Hallo Martin!
Bin durch Zufall 😉 auf diese Seite gelangt.
Nicht falsch verstehen, denn nichts liegt mir ferner als ein „Copyright“ auf Formeln, aber
=INDEX(SORTIERENNACH(SEQUENZ(49);ZUFALLSMATRIX(49));SEQUENZ(6))
wurde von mir bereits 2020, also direkt nach Freischaltung von SORTIERENNACH() als Tipp für eine Lottoziehung veröffentlicht.
https://www.clever-excel-forum.de/Thread-Lottozahlengenerator-Excel-365-oder-Online
Und da ich ein Freund von GoogleSheets bin, möchte ich auch auf das „bessere“ SORTN() verweisen:
Obige Formel kann ich dort wie folgt darstellen:
=SORTN(SEQUENCE(49);6;;RANDARRAY(49);1)
Beste Grüße
Ralf
Hallo Ralf,
dann haben die Kollegen vom Global Excel Summit, von denen ich abgeschrieben habe, möglicherweise schon von dir abgeschrieben 😉
Nein, im Ernst:
Du warst ganz offensichtlich deutlich schneller mit deiner Lösung und das soll auch erwähnt werden. Und dass du auch gleich noch eine Variante für GoogleSheets lieferst, wird den einen oder anderen Leser sicherlich freuen. Vielen Dank dafür!
Schöne Grüße,
Martin