So, lieber Excel-Freund, es ist wieder soweit: Heute gibt es den ersten Gastartikel des Jahres 2015, geschrieben von meinem geschätzten Excel-Kollegen Gerhard Pundt.
Er widmet sich einer spannenden und extrem mächtigen Excel-Funktion, die bei vielen Anwendern völlig zu Unrecht ein Schattendasein führt. Es geht um die Funktion
SUMMENPRODUKT
Gerhard hat sich so intensiv mit der Materie auseinandergesetzt, dass daraus sogar eine zweiteilige Artikel-Serie geworden ist. Keine Angst: Er hat dazu viele praxisnahe Beispiele gefunden, die dir dabei helfen werden, die Vielseitigkeit dieser mächtigen Funktion besser zu verstehen.
Und nun viel Spaß mit dem ersten Teil:
Ein bisschen Wortspalterei
Das Wort SUMMENPRODUKT erscheint auf den ersten Blick als zusammengesetztes Substantiv. Im Deutschen steht das Grundwort in einem zusammengesetzten Wort stets am Ende. Das Grundwort entscheidet den Gesamtinhalt. So könnte man meinen, es gehe bei SUMMENPRODUKT um das Produkt von Summen. Das Grundwortprinzip lässt sich z.B. beim Begriff Armbanduhren (= Art von Uhren) bzw. beim Begriff Uhrenarmband (= Teil dieser Uhren) nachvollziehen.
Dem ist bei SUMMENPRODUKT nicht so. Bei SUMMENPRODUKT werden die Elemente von Matrizen miteinander multipliziert und die Produkte anschließend summiert. Ein besseres Wort wäre deshalb vielleicht PRODUKTESUMME, aber eine Funktion mit diesem Namen gibt es nicht. Nebenbei, bei der Funktion QUADRATESUMME ist dies besser gelungen. So bleibe ich bei SUMMENPRODUKT und sehe dieses Wort nicht als zusammengesetztes Substantiv, sondern einfach als Namen für eine Funktion.
An ein paar Beispielen möchte ich zeigen, wie die Funktion arbeitet (Beispieldatei hier herunterladen). Die Funktion ist eine tolle Funktion, denn sie kann die Arbeit von mehreren Funktionen, nämlich PRODUKT, WENN bzw. SUMMEWENN bzw. SUMMEWENNS und SUMME in einem Arbeitsgang vereinen. Sie kann dennoch nicht alles. Andere Funktionen haben unvermindert ihre Existenzberechtigung.
Die Beispiele sind ausnahmslos von mir, methodisch habe ich mich allerdings ein wenig umgesehen. Die Funktion SUMMENPRODUKT gehört zur Kategorie „Mathematik und Trigonometrie“. Die Syntax lautet gemäß Excel-Hilfe:
„SUMMENPRODUKT(Matrix1;Matrix2;Matrix3; ...)
wobei Matrix1; Matrix2; … 2 bis 255 Matrizen sind, deren Komponenten wir zunächst multiplizieren und anschließend addieren möchten.“
Aus der Praxis heraus muss die Syntax auf eine zweite Schreibweise erweitert werden:
SUMMENPRODUKT(Matrix1*Matrix2*Matrix3; ...)
Beide Schreibweisen werden mit den Beispielen gezeigt.
Beispiel 1: Einspaltige Matrizen
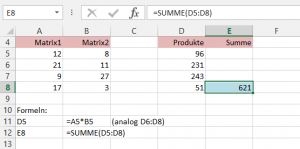
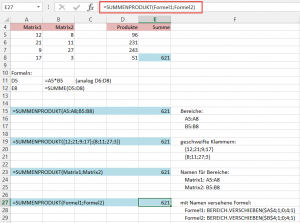
In den Spalten A und B habe ich zwei einspaltige Matrizen aufgelistet. Die Produkte daraus sind in Spalte D errechnet. In E8 schließlich habe ich die Produkte addiert:
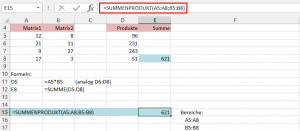
Die Funktion SUMMENPRODUKT rechnet genauso und führt zum gleichen Ergebnis:
Eine Matrix kann in Excel in folgenden Formen auftreten:
- ein Bereich, z.B. A5:A8
- eine in geschweiften Klammern gesetzte Aufzählung von Werten sein, z.B.: {12;21;9;17}
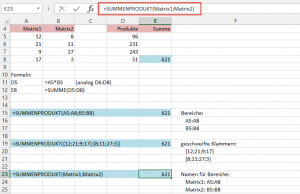
- ein Name für einen Bereich, z.B. „Matrix1“ für den Bereich A5:A8 und Matrix2 für den Bereich B5:B8
- eine mit einem Namen versehen Formel, z.B. wird im Namensmanager „Formel1“ definiert
- eine während der Berechnung erzeugte, unsichtbare Matrix (mehr dazu im Beispiel 11 in Teil 2 dieser Artikelserie)
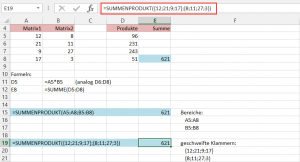
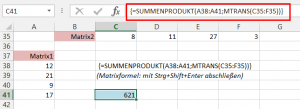
Es kann vorkommen, dass die Matrizen nicht parallel zueinander stehen:
Matrix 2 muss transponiert werden, dies geschieht mit der Funktion MTRANS. Aber Achtung, diese Funktion ist als Matrixformel mit Strg+Shift+Enter abzuschließen und ist dann von geschweiften Klammern umgeben.
MTRANS integriere ich in SUMMENPRODUKT und schließe diese Funktion dann gesamt als Matrixformel ab. Dann sieht die Formel so aus:
{=SUMMENPRODUKT(A38:A41;MTRANS(C35:F35))}
(Matrixformel: mit Strg+Shift+Enter abschließen)
Welche Variante auch gewählt wird, das Ergebnis ist das gleiche. Details dazu sind in der Beispieldatei unter Beispiel1 aufgeführt.
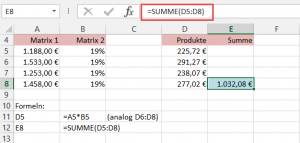
Beispiel 2: einspaltige Matrix und Konstante
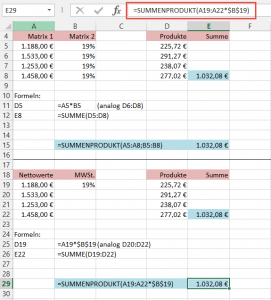
Matrix 1 enthält Nettowerte, Matrix 2 durchgängig den Wert 19%. Die Nettowerte sollen mit den 19% multipliziert, die Produkte dann summiert werden:
Die Funktion rechnet so:
=SUMMENPRODUKT(A5:A8;B5:B8) = 1.032,08 €
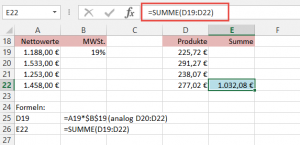
Nun gehe ich einen Schritt weiter und verzichte auf Matrix 2. Stattdessen steht in C19 die Konstante 19%:
Die Formel schreibe ich nun etwas anders. Statt Matrix und Konstante mit „;“ zu trennen (dies führt im Ergebnis zu #WERT!, setze ich an diese Stelle „*“ und multipliziere so die Matrix mit der Konstante. Schließlich wird die Summe der Produkte errechnet. Das Ergebnis stimmt mit dem vorangegangenen überein:
Beispiel 3: Die häuslichen Wasserkosten
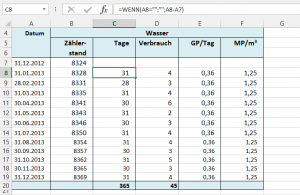
In einer Tabelle sollte jeweils das Ablesedatum und der Zählerstand eingetragen werden. Der Grundpreis / Tag (GPW bzw. GPA) und der Mengenpreis / m³ (MPW bzw. MPA) können je nach Gültigkeit schon vorgetragen sein. Datum und Zählerstand trage ich jeweils zum Ablesezeitpunkt ein:
Die Anzahl der Tage zum Ablesedatum 31.01.2013 berechne ich in C8 mit der Formel:
=WENN(A8="";"";A8-A7)
Diese Formel ziehe ich mit dem Ausfüllkästchen bis C19 runter. Die WENN-Abfrage ist notwendig, weil sonst ungewollte Negativwerte in Spalte C ausgewiesen werden. Den Verbrauch zum Ablesedatum 31.01.2013 berechne ich in D8 mit der Formel
=WENN(B8="";"";B8-B7)
und ziehe sie bis D19 runter. Die WENN-Abfrage ist auch hier zur Vermeidung von Negativwerten notwendig.
Die Tabelle ist fertig und es kann ans Rechnen gehen. Als Erstes will ich wissen, welcher Betrag insgesamt für den Grundpreis zu zahlen ist. Die Komponenten zweier einspaltiger Matrizen werden multipliziert und dann addiert.
Also: In Zeile 8 werden 31 Tage mit 0,36 €/Tag multipliziert, in Zeile 9 werden 28 Tage mit 0,36 €/Tag multipliziert usw. bis zu Zeile 19 (31 Tage multipliziert mit 0,36 €/Tag). Die zwölf Produkte werden schließlich summiert. Das ist das Prinzip von SUMMENPRODUKT.
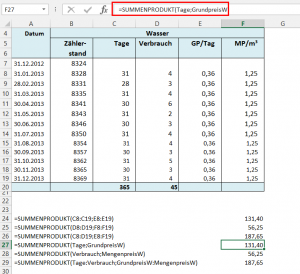
=SUMMENPRODUKT(C8:C19;E8:E19) = 131,40
Genauso verfahre ich mit der Abfrage zum Mengenpreis. Auch hier werden zwei einspaltige Matrizen multipliziert und anschließend addiert:
=SUMMENPRODUKT(D8:D19;F8:F19) = 56,25 €
Ebenso nehme ich die Abfrage zu den Gesamtkosten für Trinkwasser vor:
=SUMMENPRODUKT(C8:D19;E8:F19) = 187,65 €
In dieser Formel habe ich es nun erstmalig mit zwei zweispaltigen Matrizen zu tun, deren Komponenten zuerst multipliziert und dann addiert werden. Die erste Matrix enthält die Werte der Spalten Tage und Verbrauch, die zweite Matrix die der Spalten Grundpreis/Tag und Mengenpreis/m³.
Gerechnet wird so, z.B. in Zeile 8: 31 Tage x 0,36 €/Tag und 4 m³ x 1,25 €/m³. So gehe ich bis zur Zeile 19 vor und addiere schließlich die Einzelergebnisse. Jetzt soll ein nächster Schritt getan werden.
Für die Bereiche, die in den vorangegangenen Formeln die Matrizen bezeichnen, vergebe ich Namen:
C8:C19 Tage
D8:D19 Verbrauch
E8:E19 GrundpreisW
F8:F19 MengenpreisW
Nun rechne ich das Ganze noch einmal mit den namentlichen Angaben:
=SUMMENPRODUKT(Tage;GrundpreisW) = 131,40
=SUMMENPRODUKT(Verbrauch;MengenpreisW) = 56,25
=SUMMENPRODUKT(Tage:Verbrauch;GrundpreisW:MengenpreisW) = 187,65
Ähnliche Tabellen können auch für Abwasser oder Strom oder Gas aufgebaut und genutzt werden.
Beispiel 4: Kosten eines bestimmten Zeitraums abfragen
Mich interessieren die Kosten für Wasser oder Abwasser oder Strom oder Gas für einen bestimmten Zeitraum, z.B. für das erste Quartal.
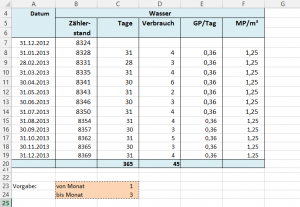
Dazu mache ich eine Vorgabe:
In den Formeln gebe ich nun die Bedingung ein, dass der Monat aus dem Datum in Spalte A größer/gleich der Vorgabe in C23 und kleiner/gleich der Vorgabe in C24 sein muss.
Die Formel zur Berechnung des Grundpreises verändert sich so:
=SUMMENPRODUKT((MONAT(A8:A19)>=$C$23)*(MONAT(A8:A19)<=$C$24)*Tage*GrundpreisW) = 32,40
Für den Mengenpreis rechne ich:
=SUMMENPRODUKT((MONAT(A8:A19)>=$C$23)*(MONAT(A8:A19)<=$C$24)*Verbrauch*MengenpreisW) = 13,75
Abschließend zu diesem Beispiel noch ein paar Formeln, die zeigen, was SUMMENPRODUKT auch kann. Die Funktion kann Summen berechnen:
=SUMMENPRODUKT(Tage) = 365
=SUMMENPRODUKT(Verbrauch) = 45
Ich will den durchschnittlichen Tagesverbrauch wissen:
=SUMMENPRODUKT(Verbrauch)/SUMMENPRODUKT(Tage) = 0,1233
Jetzt kommt ein Wahrheitswert ins Spiel. Ich will wissen, wie viel Grundpreis ich für die Monate zahle, die mehr als 30 Tage haben:
=SUMMENPRODUKT((Tage>30)*Tage*GrundpreisW) = 78,12
Hier frage ich die Summe des Produktes für nur einen Monat ab, in $F$37 steht: 31.08.2013.
=SUMMENPRODUKT((A8:A19=$F$37)*Tage*GrundpreisW) = 11,16
Zu guter Letzt habe ich die Abfrage von drei Wahrheitswerten abhängig gemacht:
- das Datum soll größer als der 31.07.2013 sein
- der Zählerstand soll größer als 8357 sein
- die Anzahl der Tage soll größer als 30 sein
Beachte bitte, dass das Zeichen „*“ „und“ bedeutet. „Und“ heißt in diesem Beispiel, es werden aus den Matrizen nur die Elemente ausgesucht, auf die obige drei Bedingungen zutreffen und dann multipliziert:
=SUMMENPRODUKT((WERT(A8:A19)>WERT("31.07.2013"))*(B8:B19>8357)*(Tage>30)*Verbrauch*MengenpreisW) = 11,25
(Hinweis: alle diese Formeln findest du auch in der Beispieldatei).
Beispiel 5: Kleiner Exkurs zur Schreibweise von logischen Abfragen
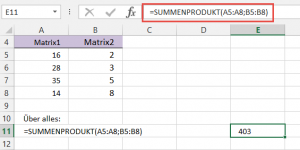
Das Beispiel zeigt zwei Matrizen mit je vier Elementen. Das SUMMENPRODUKT über alles ergibt 403:
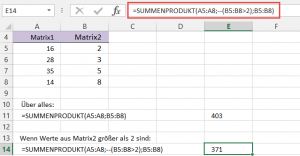
Ich will das Ergebnis wissen, das ich erhalte, wenn ich nur die Werte aus Matrix2 berücksichtige, die größer als 2 sind.
Die erste Formel verwendet ein doppeltes Minuszeichen:
=SUMMENPRODUKT(A5:A8;--(B5:B8>2);B5:B8)
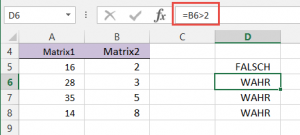
Was bedeutet das? Wenn ich in meiner Excel-Datei =B6>2 schreibe, erhalte ich WAHR:
Damit kann ich nicht rechnen. Das erste Minus macht WAHR zur Zahl -1, das zweite zu +1. Gehe ich so von B5 bis B8 vor erhalte ich zunächst FALSCH;WAHR;WAHR;WAHR, dann 0;1;1;1. Diese Werte multipliziert SUMMENPRODUKT nun mit Matrix1 und Matrix2. Die Summe ergibt 371.
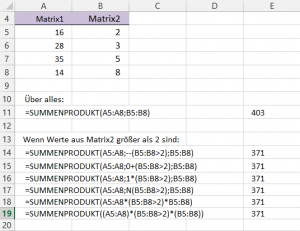
Die zweite Formel ersetzt das doppelte Minuszeichen durch „0+“. Ich erhalte wieder 0;1;1;1. Multipliziert mit den Werten aus beiden Matrizen ergibt die Summe wieder 371:
=SUMMENPRODUKT(A5:A8;0+(B5:B8>2);B5:B8)
In der dritten Formel schreibe ich statt „0+“ nun „1*“. Das Ergebnis ist 371:
=SUMMENPRODUKT(A5:A8;1*(B5:B8>2);B5:B8)
Die vierte Formel setzt statt „1*“ die Funktion N vor B5:B8>2. Die N-Funktion wandelt WAHR in 1 und FALSCH in 0 um. Ich erhalte wieder 371:
=SUMMENPRODUKT(A5:A8;N(B5:B8>2);B5:B8)
Formel 5 und Formel 6 sind fast identisch. Sie unterscheiden sich nur dadurch, dass A5:A8 bzw. B5:B8 einmal ohne und einmal mit Klammern geschrieben werden:
=SUMMENPRODUKT(A5:A8*(B5:B8>2)*B5:B8)
=SUMMENPRODUKT((A5:A8)*(B5:B8>2)*(B5:B8))
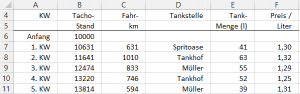
Beispiel 6: Tanken
Als kostenbewusster Autofahren führe ich genau Buch, wie viel ich wann, wo und zu welchem Literpreis getankt habe. Hier sieht man einen Auszug aus der Beispieldatei:
Zuerst interessiert mich, welche Kosten ich in den zehn Kalenderwochen gesamt hatte. Dazu rechne ich:
=SUMMENPRODUKT((E7:E16)*(F7:F16)) = 692,49
Als nächstes interessiert mich, welche Kosten ich ab km-Stand 12474 gehabt habe. Dazu füge ich diese Bedingung in die vorangegangene Formel ein:
=SUMMENPRODUKT((B7:B16>12474)*(E7:E16)*(F7:F16)) = 485,08
Jetzt will ich noch wissen, wie viel Geld ich ab km-Stand 12474 bei der Tankstelle Tankeschön gelassen habe. Auch das ist nicht so schwierig:
=SUMMENPRODUKT((B7:B16>12474)*(D7:D16="Tankeschön")*(E7:E16)*(F7:F16)) = 129,66
Zum Schluss interessiert mich noch der Durchschnittsverbrauch pro 100 km. Dazu verwende ich die Funktion so:
=SUMMENPRODUKT((E7:E16)/(C7:C16)*100)/ANZAHL2(A7:A16) = 6,5
Beispiel 7: Planwerte und Wachstum
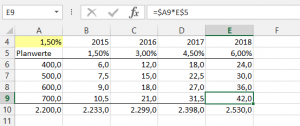
Meine Ausgangstabelle zeigt Spalte A Planwerte für z.B. den Umsatz von vier Produkten. Darüber steht mit 1,5% das angestrebte jährliche Wachstum. Die Spalten sind beschriftet mit den folgenden Planjahren und dem kumulierten Wachstum:
Im Bereich B6:E9 wird nun zeilenweise das Wachstum im Planjahr zum jeweiligen Prozentsatz berechnet.
Mit SUMMENPRODUKT frage ich zunächst ab, um welchen Betrag der Planumsatz bis 2018 insgesamt steigt.
=SUMMENPRODUKT((B5:E5)*$A$10) = 330,0
Will ich das für das Jahr 2016 wissen, schreibe ich B5:C5 usw.
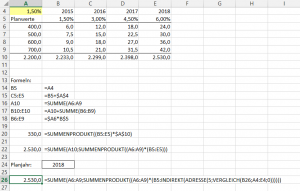
Abfragen kann ich auch, wie hoch der Umsatz bei den angenommenen Wachstumsraten in 2018 sein wird:
=SUMME(A10;SUMMENPRODUKT((A6:A9)*(B5:E5))) = 2.530,0
Will ich das Abfragejahr dynamisch in die Formel einbringen (mit Zelle B26 schaffe ich mir dazu eine Auswahlmöglichkeit), schreibe ich so:
=SUMME(A6:A9;SUMMENPRODUKT((A6:A9)*(B5:INDIREKT(ADRESSE(5;VERGLEICH(B26; A4:E4;0)))))) = 2.530,0
Fortsetzung folgt…
Über den Autor
Ich heiße Gerhard Pundt, bin 59 Jahre alt, verheiratet und habe Betriebswirtschaft studiert.
Seit ca. 15 Jahren arbeite ich in einem Unternehmen der Wasserver- und Abwasserentsorgung in Mecklenburg-Vorpommern als Controller.
Zu Excel kam ich 1993, bedingt durch die Arbeit. Mein heutiges Wissen in Excel und VBA habe ich mir autodidaktisch durch Lesen, Probieren und Üben angeeignet.
Heute kann ich sagen: Ich weiß mir zu helfen.
Was mache ich sonst noch gern? Ich lese Romane, inzwischen auch digital mit einem Ebook-Reader.
So, das war der erste Teil in der Artikelserie zur SUMMENPRODUKT-Funktion in Excel. Ich denke, das sollten wir jetzt erst mal eine Weile sitzen lassen. Und nächste Woche gibt es hier den zweiten Teil mit weiteren interessanten Beispielen und Anwendungsfällen.

P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.






Hallo Martin,
eine Frage zur Funktion „Summe“. Wenn ich mehrere Tabellenblätter, hier als Beispiel Monate, in ein Blatt zusammenaddieren will, dann gebe ich ein: =Summe(Januar:Dezember!A1) ein. Funktioniert auch problemlos. Nur warum funktioniert dieser Befehl nicht, wenn die Tabellenblätter alle nach KW benannt sind? =Summe(KW 1:KW 52!A1) erhalte ich immer eine Fehlerwarnung.
Hallo Lars,
der Grund liegt darin, dass die Namen der Tabellenblätter ein Leerzeichen enthalten. Daher müssen sie in der Formel in einfache Anführungszeichen gesetzt werden:
=SUMME(‚KW 1:KW 52‘!A1)
Damit funktioniert’s.
Schöne Grüße,
Martin
Pingback: So lässt sich die Funktion SUMMENPRODUKT nutzen, 13 Fälle | clevercalcul
Hallo Martin
ich habe eine Frage zu Beispiel 4:
B28 = 01.11.2016
C28 = 30.11.2016
Tabelle 11 Spalte D = Datumsformat (42704.43325) oder umgewandelt 30.11.2016
=SUMMENPRODUKT((’11‘!D:D>=B28)*(’11‘!D:D<=C28))
zeigt mir einen Wert von 0 an, obwohl da 1 Eintrag vorhanden ist.
Wenn ich das Datum dort auf den 29.11.22016 ändere, wird es gezählt.
Auch eine Anpassung auf D2:D1000 hat nichts gebracht.
kleiner/gleich C28 sollte den 30.11. aber mit einbeziehen.
ich seh den Fehler nicht.
Kannst Du mir da weiterhelfen ?
Hallo Jürg,
das Problem bei Datumswerten tritt auf, wenn Uhrzeiten im Spiel sind. Der von Dir angegebene Wert (42704,43325) heißt genau genommen „30.11.2016 10:23:53“
Und das ist eben nicht exakt dasselbe wie 30.11.2016. Nimm die Uhrzeit raus und es sollte klappen.
Schöne Grüße,
Martin
Hallo Martin
ich habe sogar noch eine andere Lösung dazu gefunden:
mein Suchbereich liegt jetzt jeweils zwischen dem 01.11.2016 und 01.12.2016 somit funktioniert es auch.
Vielen Dank für Deine Antwort.
Pingback: Zählen und addieren mal ganz anders | Der Tabellen-Experte
Hallo Martin,
ich bin am Verzweifeln. Nach tagelangem „basteln“ gebe ich auf.
Mein Problem: ich habe eine Tabelle mit Umsätzen von mehreren Personen. Nun will ich den Umsatz einer Person aus einem Monat berechnen. Meine Formel, die den Umsatz des Mitarbeiters „K“ für Januar 2017 berechnen sollte, gibt jedoch nur „WERT“ zurück.
=SUMMENPRODUKT((TEXT($B$3:$B$90;“K“)*TEXT($P$3:$P$90;“MM.JJ“)=“01.17″)*$N$3:$N$90)
Spaltenerklärung: B=Person, P=Datum und N=Umsatz
Wo ist das Haar in der Suppe?
Vielen Dank schon mal im Voraus.
Schöne Grüße
Kurt
Hallo Kurt,
versuch’s mal hiermit:
=SUMMENPRODUKT(–(($B$2:$B$89)=“K“)*–(TEXT($P$2:$P$89;“MM.JJ“)=“01.17″)*$N$2:$N$89)
Schöne Grüße,
Martin
Hallo Martin,
danke für deine Zeit. Leider sagt mir das Ergebnis #NAME. Hast du vielleicht noch eine andere Idee. Ich habe mit Summewenns versucht, leider ohne Ergebnis.
Die Formel zur Errechnung des Einzelumsatzes monatlich ist doch in den Buchhaltungsprogrammen auch enthalten. Ich dachte, das geht „mit links“.
Viele Grüße
Kurt
Hallo Kurt,
ich vermute, Du hast die Formel oben per Copy&Paste eingefügt. Das Problem hier auf der Webseite ist, dass nicht alle Zeichen sauber angezeigt werden: Der lange Strich hinter „=SUMMENPRODUKT(“ sind eigentlich zwei Minuszeichen, ebenso der lange Strich vor „(TEXT“
Dann sollte es klappen.
Schöne Grüße,
Martin
Hallo, ich beschäftige mich schon länger mit der Funktion „Summenprodukt“ – bei einer Sache komme ich aber nicht weiter:
Ich möchte in der Formel Summenprodukt den Bereich von der 3. Zeile bis zur letzen Zeile abdecken. Das Problem ist, das die letzte Zeile sich jeden Tag verschiebt (die Tabelle wird jeden Tag einige Zeilen länger). Mit A:A bzw. 1:1 (für Spalte oder Zeile) komme ich nicht weiter. Gibt es hierür eine Lösung.
Wäre nett, wenn Sie mir hier „auf die Sprünge“ helfen könnten.
Vielen Dank
Frank Osterrieder
Hallo Herr Osterrieder,
für solche Fälle empfehle ich, anstelle von Zellbezügen dynamische Bereichsnamen zu verwenden. Wie man so einen Namen anlegt, habe ich in diesem Artikel beschrieben:
Jetzt kommt Bewegung rein: Dynamische Bereichsnamen
Ein anderer grundsätzlich empfehlenswerter Ansatz sind formatierte Tabellen. Damit erhalten Sie automatisch dynamisch angepasste Bereiche und können in Ihren Formeln mit sogenannten strukturierten Verweisen arbeiten. Hier ebenfalls ein Artikel dazu:
Ordnung ins Chaos bringen: Strukturierte Verweise
Schöne Grüße,
Martin
Hallo Martin,
in der Beispieldatei im Blatt: Beispiel 6 gibt es eine weitere Formel für den durchschnittlichen Verbrauch auf 100km:
=SUMMENPRODUKT(E7:E16)/SUMMENPRODUKT(C7:C16)*100 . Mit dieser Formel erhalte ich das gleiche Ergebnis als würde ich es zu „Fuß“ ausrechnen:
=(SummeTankmenge [548] /SummeFahrkm [8405] )*100) => 6,5199
Mit der anderen Formel: =SUMMENPRODUKT((E7:E16)/(C7:C16)*100)/ANZAHL2(A7:A16) ist das Ergebnis abweichend =>6,5369. Nun stellt sich mir die Frage WARUM? Vielleicht habe ich einen Denkfehler oder die Formel ist „kaputt“ 😉 Eventuell können Sie mir diese unterschiedlichen Ergebnisse erklären.
Lieben Dank & sonnige Grüße
Steffi
Hallo Steffi, deine erste Formel ist richtig. In der zweiten Formel, wie sie auch in der Erklärung verwendet wurde, ist leider ein kleiner Denkfehler: der Durchschnitt der Einzeldurchschnitte ergibt leider nicht den Gesamtdurchschnitt, da sie nicht gewichtet sind. Dazu ein Bsp: Ich fahre 100km mit 20l und 1000km mit 50l. Das sind einzeln 20l/100km und 5l/100km. Bilde ich daraus den Mittelwert erhalte ich 12,5l. Die 100km fallen aber kaum ins Gewicht und es sind eigentlich 6,37l/100km (70l/1100km*100) verbraucht worden. Dass die Werte in der Erklärung des Summenproduktes fast identisch waren (ca. 6,5l/100km), ist Zufall.
Hallo,
ich habe ein Problem in Excel mit der Division Summenprodukt Formel.
Im Prinzip ist es ganz einfach. Es gibt eine Spalte mit Mengen und eine Spalte mit der Angabe „Stück/Karton“. Um keine Fehlermeldung #DIV0 zu erhalten, sind alle Zellen der Spalte gefüllt (bei Zwischenüberschriften wurde eine „1“ eingetragen).
Die Formel funktioniert leider nur, so lange bei den Mengen kein „“ eingetragen ist. Die Mengen werden über eine Formel ermittelt (wenn X>Y dann Z oder „“). Wenn nun eine Zelle mit „“ gefüllt ist erhalte ich als Ergebnis #Wert.
Selbst mit der Erweiterung „(C2:C7>0)*1“ etc. ist es mit nicht gelungen.
Kann mir hier jemand helfen?
Hallo Anke,
wie sieht denn die SUMMENPRODUKT-Formel aus, die du momentan verwendest? Momentan kann ich mir noch nicht so recht vorstellen, was du genau berechnen möchtest.
Schöne Grüße,
Martin
Hallo Martin,
ich möchte die theoretische Kartonanzahl zu einer Artikelaufstellung ermitteln. Derzeit lautet meine Formel =AUFRUNDEN(SUMMENPRODUKT(C3:C11/B3:B11);0)
Die Tabelle enthält auch Zwischenüberschriften. Die Spalte mit der Kartoneinheit habe ich immer gefüllt. In den Zeilen mit Überschrift steht in der Spalte Kartoneinheit dann eine „1“, so dass ich kein Problem mit dem Fehler #DIV0 habe.
Mein Problem ist die Mengenspalte. Die Mengen werden über eine Formel ermittelt. Hier kann es auch vorkommen, dass der Vorschlag „“ lautet (wenn ein Artikel im Vorjahr beispielsweise nicht verkauft wurde).
Selbst wenn ich statt der Formel nur die Werte in die Matrix einfüge, erhalte ich die Fehlermeldung #WERT.
Erst wenn ich die leeren Zellen gelöscht habe, erhalte ich ein Ergebnis.
Hier suche ich eine Lösung, wie ich diese Problem umgehen kann. Meine Versuche die Spalte C (Mengen) auf Werte Größer 0 zu begrenzen und dann durch die Spalte B zu teilen sind leider gescheitert 🙁
Hallo Anke,
das Problem mit dem Vergleich > 0 ist, dass auch ein durch eine Formel gesetzter leerer Eintrag in Excel einem Wert größer Null entspricht. Du könntest stattdessen prüfen, ob es sich beim Zellinhalt um eine Zahl handelt. Und wenn nicht, soll die Formel stattdessen den Wert 0 annehmen:
=SUMMENPRODUKT(WENN(ISTZAHL(C3:C11);C3:C11;0)/B3:B11)
Oder du sorgst dafür, dass die Formel, welche die Mengen ermittelt, bei einer nicht vorhandenen Menge anstatt „“ eben eine 0 reinschreibt.
Schöne Grüße,
Martin
Hallo Martin,
da hab ich so vieles versucht und die Lösung ist doch so einfach.
Danke, jetzt klappt es.
=AUFRUNDEN(SUMMENPRODUKT(WENN(ISTZAHL(C3:C11);C3:C11;0)/B3:B11);0)
Die Formel muss aber über Strg+Umschalt+Enter bestätigt werden, sonst lautet das Ergebnis 0.
Liebe Grüße
Anke
PS: Das mit der 0 statt „“ wollte ich bewusst nicht.
Hallo Martin!
Herzlichen Dank für Deine vielen Infos.
Zu Wasserkostenabrechnung habe ich noch eine Frage (die Beispieldateien können übrigens nicht mehr runtergeladen werden???):
Du hast für die Berechnungen der Kosten unter der Bedingung von Zeiträumen
=SUMMENPRODUKT((MONAT(A8:A19)>=$C$23)*(MONAT(A8:A19)=$C$23)*(MONAT(A8:A19)=$D$26)*(MONAT(Datum)=$D$26)*MONAT(Datum<=$D$27)*Verbrauch*Mengenpreis))
DATUM ist bei mir der benamte Spaltenbereich für A8:A19!
(ich weiß…gefährliche Namensvergabe da es auch eine Funktion Datum gibt)
Aber irgendwie komme ich nicht auf die 46,15 € … Wo ist mein Denkfehler?
Kleine Korrektur meinerseits:
Da war unter
„(Hinweis: alle diese Formeln findest du auch in der Beispieldatei).“
wohl einen alten Downloadlink der mich zu https://dl.dropboxusercontent.com/u/2890127/Tabellenexperte/B_SUMMENPRODUKT.xlsx und einer Fehlermeldung der Dropbox führte.
An anderer Stelle habe ich den aktuellen link gefunden
Hallo Michael,
danke für den Hinweis auf den alten Downloadlink. Ich musste mir vor längerer Zeit schon einen neuen Ablageort suchen und habe offensichtlich noch einige Links übersehen. Werde sie gleich mal anpassen.
Schöne Grüße,
Martin
Kein Thema …
Aber hast Du einen Lösungsansatz für meine Frage?
Hallo Michael,
der Artikel stammt nicht von mir, sondern von einem Gastautor. Aber ich kann im Augenblick deiner Formel auch nicht folgen. Woher kommt die? Im Artikel ist sie jedenfalls nicht vorhanden (oder ich bin blind). Und die besagten 46,15 Euro finde ich auch nirgends. Ich stehe grad auf dem Schlauch…
Schöne Grüße,
Martin
Moin Martin,
ich bin schon seit zwei Stunden am Probieren wie ich das machen soll.
Mein Problem war eine Summe bilden mit 2 Bedingungen aus einer Tabelle mit strukturierten Verweisen in eine zweite Tabelle.
Da ist im Gegensatz zu SUMMEWENNS, die nicht funktioniert, SUMMEPRODUKT, die fähigere von beiden.
Die hier vorgestellte Lösung, die Bedingungen per UND im Array zu verknüpfen, ist genial.
—————-
Kurz ein minimalisiertes Beispiel:
Ich habe eine Tabelle1 (Kosten) mit den Feldern (Datum,Kategorie,Preis),
in der alle Kosten eingetragen werden.
Ich habe eine Tabelle2 (Übersicht) mit den Feldern (Kategorie, 1, 2, …, 12),
die die Kosten in Kategorie und Monate aufschlüsselt.
für die Spalte „1“ (Januar) in Tabelle2 wäre dann diese Formel nötig gewesen:
=SUMMEWENNS(Kosten[Preis];Monat(Kosten[Datum]);1;Kosten[Kategorie];[@Kategorie])
aber die interpretiert Excel als defekte Formel!
hingegen diese Formel klappt:
=SUMMENPRODUKT(Kosten[Preis]*(MONAT(Kosten[Datum])=1)*(Kosten[Kategorie]=[@Kategorie]))
nachtrag:
Ich hätte gerne auch statt dem Wert 1 in der Formel gleich die Tabellenüberschrift des Monats genommen,
dann würde in jeder Zelle das gleiche stehen, in etwa so:
=SUMMENPRODUKT(Kosten[Preis]*(MONAT(Kosten[Datum])= [@#Kopfzeilen] )*(Kosten[Kategorie]=[@Kategorie]))
aber struktierte Verweise geben das leider nicht her, was wirklich schade ist.
—————–
Danke für den Lösungsweg!
gruss ft
Hallo ft,
die SUMMEWENNS-Funktion klappt hier nicht, da du versuchst, im Bereichsargument gleichzeitig schon die MONAT-Funktion einzusetzen. Das haut einfach nicht hin.
Die strukturierten Verweise können manchmal ein wenig tückisch sein, aber es würde schon klappen. Du musst nur den Monat der Tabellenüberschrift in einen Wert umwandeln (in formatierten Tabellen sind die Überschriften immer Text). Und wenn du die Spalten auf die folgende Weise fixierst, kannst du die Formel auch einfach in die anderen Spalten kopieren:
=SUMMENPRODUKT(Kosten[[Preis]:[Preis]]*(MONAT(Kosten[[Datum]:[Datum]])=WERT(Übersicht[[#Kopfzeilen];[1]]))*(Kosten[[Kategorie]:[Kategorie]]=@Übersicht[[Kategorie]:[Kategorie]]))
Schöne Grüße,
Martin
Hallo Martin!
Gibt es eine Möglichkeit, SUMMENPRODUKT mit MAX pro Zeile zu kombinieren? Ich möchte die Differenzen zu 30 summieren:
32 -> 2
29 -> 0
31 -> 1
Das geht: =SUMMENPRODUKT((A1:A3>30)*(A1:A3-30)) -> 3.
Aber wieso geht das hier wohl nicht? =SUMMENPRODUKT(MAX(A1:A3-30;0)).
Hallo Michael,
der Grund dafür ist, dass die MAX-Funktion für sich ja nur einen einzigen Wert zurückliefert, nämlich das Maximum. Du kannst das sehr einfach nachprüfen, in dem du die Formelauswertung aktivierst: Menü Formeln | Formelauswertung, und dann schrittweise auf die Auswerten-Schaltfläche klicken und die Berechnungsergebnisse anschauen.
Schöne Grüße,
Martin
Hallo Martin!
habe auch ein kleines Excel-Problem und hoffe du kannst mir helfen. Finde einfach keine Lösung.
Habe eine Personalstatistik mit Geschlecht, Alter, Angestellte/Beamte und möchte daraus eine neue Tabelle generieren,
die in Altersgruppen (65 – 56, 55-46, 45-36, 35-26, 25-18), Männlich oder weiblich unterteilt sind.
=SUMMENPRODUKT((Auswertung!$AA$12:$AA$220=“m“)*(Auswertung!$R$12:$R$220>=46)*(Auswertung!$R$12:$R$220<=55)*(Auswertung!$AV$12:$AV$214="A"))
Ergebnis ist immer #NV.
Durch die Umstellung auf Office 2010 funktioniert die Formel nicht mehr. Was kann ich ändern?
Vielen lieben Dank im Voraus.
Hallo Melly,
ich tippe mal darauf: du verwendest einen unterschiedlich großen Zellbereich im letzten Teil der Formel: $AV$12:$AV$214 (statt $AV$12:$AV$220)
Schöne Grüße,
Martin
Hallo Martin,
eine sehr gute Einfürhung in Summenprodukt! Dein „Beispiel 7: Planwerte und Wachstum“ finde ich sehr aufschlussreich. Dazu zwei Anmerkungen. Erstens müsste m.E. Dein Bezug auf B26 im VERGLEICH B24 lauten und zweitens funktioniert die hier vorgestellte Formel nicht mehr, wenn man die Beispieldaten ausschneidet und z.B. um 4 Spalten verschiebt. Weist Du Dir darauf einen Reim zu machen?
Gruß
Thomas
Hallo Thomas,
gerne, aber die Lorbeeren gehen hier an den Gastautor Gerhard Pundt, den diesen Artikel verfasst hat 🙂
Trotzdem von mir eine Antwort auf die beiden Fragen zum Beispiel 7:
In der Beispieldatei, die man oben im Artikel herunterladen kann, steht zum Beispiel 7 das Planjahr in Zelle B26. Daher ist der Bezug in der VERGLEICH-Funktion auf B26 schon richtig.
Und was die fehlerhafte Formel beim Verschieben angeht: Das kommt daher, dass innerhalb der ADRESSE-Funktion die letzte Datenspalte über die VERGLEICH-Funktion bestimmt wird. Diese Funktion liefert aber immer die relative Position zurück. Das heißt, die Position innerhalb des angegebenen Bereichs. Und diese Positionsnummer wird dann als Spaltennummer in der ADRESSE-Funktion verwendet.
In der Beispieldatei wird das Jahr 2018 im Bereich A4:E4 gesucht und das Ergebnis ist 5, was der Spalte F entspricht. Wenn man den Datenbereich aber beispielsweise um 6 Spalten nach rechts verschiebt (also in die Spalten H:L), lautet das Ergebnis der VERGLEICH-Funktion trotzdem 5. Aber das entspricht natürlich nicht mehr der absoluten Spaltennummer.
Du musst also zum Ergebnis der VERGLEICH-Funktion die entsprechenden Wert addieren, um den der Datenbereich verschoben wurde. Das würde dann beispielsweise so aussehen:
=SUMME(H6:H9;SUMMENPRODUKT((H6:H9)*(I5:INDIREKT(ADRESSE(5;VERGLEICH(B26;H4:L4;0)+7)))))
Schöne Grüße,
Martin
Lieber Martin,
ich bin auf der Lösungssuche im Netz auf Deiner Seite gelandet. Vielleicht kannst Du mir weiterhelfen?
Ich habe mir eine Excel-Tabelle gemacht mit zuerst folgender Bedingung: Werte mir nur in Spalte C die Zellen aus, wo daneben in Spalte D die Zahl 10 steht und zeige mir das zusammengezählte Gesamtergebnis. Das ist die Formel dafür:
=C4+SUMMENPRODUKT(($C$6:$C$3002)*($D$6:$D$3002=10))
Das funktioniert bestens. Als nächsten Schritt habe ich in dieser Gesamtsumme auch zwei weitere Zahlen in Spalte D mit dazugenommen, nämlich die Zahl 200 und 202, so das die Summen berechnet werden, sobald Spalte D entweder 10, 200 oder 202 ist. Die Formel dafür sieht so aus:
=C4+SUMMENPRODUKT(($C$6:$C$3002)*($D$6:$D$3002=10))+SUMMENPRODUKT(($C$5:$C$3002)*($D$5:$D$3002=200))+SUMMENPRODUKT(($C$5:$C$3002)*($D$5:$D$3002=202))
Funktioniert ebenfalls bestens.
Wenn ich jetzt 13 weitere, als nur die drei, dazunehmen will, dann wird´s unübersichtlich. Dann hätte ich statt 3x wie oben mit 10,200,202 nun insgesamt 16 x das gleiche Summenprodukt mit jeweils der anderen Zahl am Ende darin. Das würde funktionieren, aber eine elend lange Formel geben.
Kann man beliebige Zahlen in eine kleinen Formel einpassen, wie zB.
=C4+SUMMENPRODUKT(($C$6:$C$3002)*($D$6:$D$3002=10+20+22+24+26+28+30+32+34+36+38+40+42+44+200+202)).
Natürlich funktioniert diese Formel so nicht, aber ich wollte nur illustrieren, wie ich das meine. Geht das überhaupt die Formel zu kürzen, oder muss ich 16x =C4+SUMMENPRODUKT(($C$6:$C$3002)*($D$6:$D$3002=xx))+ mit der entsprechender Zahl bei xx hintereinander schreiben?
Schon mal vielen Dank für die Antwort.
Liebe Grüße
Karsten
Moin Karsten
Wenn ich dich richtig verstanden habe, würde ich das so machen:
=C4+SUMMENPRODUKT(($C$6:$C$3002)*($D$6:$D$3002={10.20.22.24.26.28.30.32.34.36.38.40.42.44.200.202}))
Achte dabei auf die geschweiften Klammern im letzten Teil der Formel.
Gruß Marcel
Hallo Marcel,
endlich Wochenende. Ich kriege von Corona nichts mit, mein Überstundenkonto steigt gerade wieder an. Daher erst jetzt die Antwort.
Du hast völlig richtig verstanden. Deine Lösung: BINGO!!! Genau nach dem habe ich gesucht. Super! Danke, vielen Dank für Deine Hilfe!!! Werde gleich im Anschluß an meiner Excel-Datei weiterschreiben. Wenn Du in meiner Ecke wohnen würdest (südl. Darmstadt) hätte ich Dich jetzt auf´n Bier eingeladen 🙂
Gruß
Karsten