Letzte Woche hatte ich mit der RMZ-Funktion gezeigt, wie hoch die regelmäßigen Zahlungen sein müssen, um ein bestimmtes Ziel zu erreichen (z.B. Darlehen abbezahlen, Kapital ansparen etc).
Heute stelle ich eine verwandte Excel-Funktion aus der Finanzmathematik vor, die etwas anders gelagerte Fragestellungen beantworten soll:
- Wie hoch muss mein Vermögen sein, um für eine bestimmte Zeit eine fixe Rente bezahlt zu bekommen
- Wie hoch könnte ein Darlehen sein, wenn ich einen bestimmten monatlichen Betrag zur Rückzahlung aufbringen kann
- Welchem heutigen Betrag entspricht eine zukünftige Investition bei einer gegebenen Verzinsung
usw.
Die Antworten auf diese und ähnliche Fragen liefert die Barwert-Funktion. Und so geht’s:
Die BW-Funktion
Zu Beginn wieder etwas Theorie:
Die BW-Funktion gibt den Barwert einer Investition zurück, also den heutigen Gesamtwert einer Reihe zukünftiger Zahlungen.
Die allgemeine Syntax sieht wie folgt aus:
=BW(Zins; Zzr; Rmz; [Zw]; [F])
Zins:
Das ist der Zinssatz pro Periode bzw. Zahlungszeitraum. Da Zinssätze üblicherweise für 1 Jahr angegeben werden, muss bei monatlichen Zahlungen der Zinssatz durch 12, bei vierteljährlichen Zahlungen durch 4 usw. geteilt werden.
Zzr:
steht für Zahlungszeiträume. Damit gibt man an, wie oft die jeweilige Annuität oder Rente gezahlt werden soll. Wichtig dabei ist nur, dass die Zinszeiträume und die Zahlungszeiträume zueinander passen. Das heißt, wenn man mit monatlichen Zahlungen arbeiten möchte, dann muss auch der Zinssatz auf einen Monat gerechnet werden.
Rmz:
ist der konstante Betrag, der in jeder Periode bezahlt wird (Rmz = Regelmäßige Zahlungen). Man spricht hier auch von einer Annuität. Im Falle eines Darlehens setzt sie sich zusammen aus dem Zinsanteil und dem Tilgungsanteil.
Zw:
Der zukünftige Wert ist der Endwert, den man nach der letzten Zahlung erreicht hat. Dieser Parameter ist optional, kann also auch weggelassen werden. Der angenommene Endwert ist dann Null.
F:
Damit gibt man die Fälligkeit an: 1 bedeutet, die Zahlung ist zu Beginn der Periode fällig, 0 (Null, oder nicht angegeben) bedeutet, die Zahlung ist am Ende der Periode fällig.
Schauen wir uns wieder ein paar praktische Anwendungsfälle an.
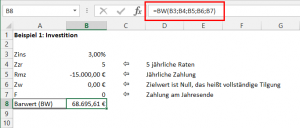
Beispiel 1: Investition
Angenommen, unser Chef will sich zur Ruhe setzen und wir wollen ihm seinen kleinen Handwerksbetrieb abkaufen. Dafür sollen wir ihm in den nächsten 5 Jahren jeweils am Jahresende 15.000,- Euro zahlen. Insgesamt also 75.000,- Euro.
Wie hoch wäre die Investitionssumme, die wir heute komplett auf den Tisch legen müssten, wenn wir mit einem angenommenen Zins von 3% rechnen würden?
Die BW-Funktion liefert die Antwort:
Die (zukünftigen) 75.000 Euro Investitionssumme entsprechen unter den oben genannten Bedingungen also einem (heutigen) Barwert von 68.685 Euro.
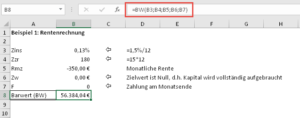
Beispiel 2: Rente
Wir überlegen uns, unsere zukünftige Rente etwas aufzubessern. Dazu haben wir bis zum Rentenbeginn ein Kapital von 50.000 Euro angespart und wollen uns davon über die nächsten 15 Jahre jeweils 350,- Euro monatlich auszahlen lassen. Die Guthabensverzinsung liegt bei angenommenen konstant mikrigen 1,5%. Reicht unser angespartes Kapital dafür aus?
Leider nein! Die BW-Funktion zeigt, dass wir bei Auszahlungsbeginn mindestens 56.384 Euro auf der hohen Kante haben müssten:
Hinweis:
Die angegebenen Beispiele sollen lediglich eine Idee davon geben, wofür man die BW-Funktion grundsätzlich brauchen kann. Dass im wahren Leben die Guthabenszinsen nicht über einen so langen Zeitraum konstant bleiben, wird hier ebensowenig berücksichtigt wie der Faktor Geldentwertung/Inflation.
So, dass war jetzt der zweite Teil der kleinen dreiteiligen Serie über Finanzmathematische Funktionen in Excel. Im dritten und letzten Teil werde ich die Funktion ZZR vorstellen, mit der man Laufzeiten berechnen kann.

P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.






Super hilfreich. Ich vergesse die Formeln von einem auf’s andere Mal – trotz Hilfefunktion.
In dem zweiten Beispiel ist ein Fehler, in der Aufgabenstellung ist die Rede von 300€ monatlich, in der Lösung steht dann plötzlich 350€. 🙂
Aber super gut erklärt!
Hallo Selina,
Pfusch am Bau! Danke für den Hinweis, habe ich gleich mal korrigiert 🙂
Schöne Grüße,
Martin
Beim Beispiel 2 wurde bei F 0 angegeben, obwohl am Monatsanfang steht.
Hallo AM,
vielen Dank für den Hinweis, ich habe die Beschriftung im Bild 2 jetzt korrigiert.
Schöne Grüße,
Martin