Heute kommt wieder einmal ein Gastautor zu Wort: Martin Fuchs, seines Zeichens Analyst und Controller und somit ein Parade-Excel-Anwender, hat sich einige Gedanken zur Funktion ZUFALLSZAHL() gemacht.
Er zeigt, wie man sich mit dieser und ein paar anderer Excel-Funktionen der Kreiszahl Pi nähern kann. Das dabei zur Veranschaulichung erstellte Diagramm wird auch die mathematischen Abstinenzler unter uns auf jeden Fall ansprechen.
Vielen Dank an Martin Fuchs für diesen schönen Beitrag!
Und los geht’s:
In diesem Artikel möchte ich eine weitere kreative Möglichkeit zur Nutzung der Excel-Funktion ZUFALLSZAHL() aufmerksam machen. Die Idee dazu kam mir, als ich bei Wikipedia den Artikel zur Kreiszahl Pi las, und dort auf das Buffonsche Nadelproblem stieß.
Im Prinzip geht es darum, durch eine zufällig entstandene Verteilung – bei Buffon sind es Stöckchen die auf Fugen von Kacheln landen – auf Pi zurückzuschließen. Excel kann zufällige Verteilungen recht gut und warum nicht per Zufall Punkte auf ein Koordinatensystem „schießen“?
Wenn wir also mit Excel ganz simpel 2 Koordinaten innerhalb eines Koordinatenquadrats der Länge r auswürfeln, dann liegt eine gewisse Anzahl davon außerhalb des gedachten Kreises mit Radius r, und eine andere Anzahl innerhalb des Kreises.
Das Verhältnis aller zufällig generierten Punkte innerhalb des gedachten Kreises zu allen zufällig generierten Punkten insgesamt geht gegen ¼ von Pi je mehr man sich unendlich vielen Versuchen nähert. Ein Viertel deshalb, weil wir unser Experiment mit nur einem viertel Kreis veranstalten.
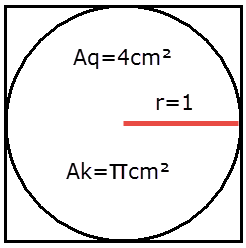
Warum ist das so? Nun, ein Kreis mit Radius r passt genau in ein Quadrat der Kantenlänge 2r, der Flächeninhalt eines Kreises ist πr² und für einen Kreis mit Radius 1 genau π cm².
Das Quadrat um einen Kreis mit Radius 1 hat 4 cm², also ist das Verhältnis für einen ganzen Kreis π:4 und in unserem Koordinatensystem also innerhalb des Viertelkreises ¼π:1.
Natürlich war ich nicht der Erste, der eine so offensichtliche Idee hatte, es brauchte nur eine Google-Suche, um festzustellen, dass diese Methode sogar einen eigenen Namen hat: Der Monte Carlo Algorithmus
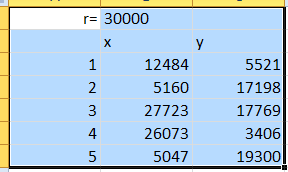
Zurück zu Excel und dem Versuch mit der ZUFALLSZAHL() Funktion etwas Nettes zu basteln: In meinem Beispiel lasse ich den Benutzer entscheiden, welchen Radius sein Kreis bzw. welche Kantenlänge sein Koordinatensystem haben soll, die Eingabe erfolgt in Zelle B1:
Daraufhin werden die Koordinaten in den Spalten B und C generiert, wobei ich die Spalte A zur Nummerierung benutzt habe, in allen Zellen finden wir die selbe Formel, die da lautet:
=AUFRUNDEN(ZUFALLSZAHL()*$B$1;0)
Achtet hierbei darauf, über F4 die Dollarzeichen um B1 (=$B$1) zu erzeugen, denn man braucht unbedingt den absoluten Bezug auf immer dieselbe Zelle, nämlich den vom User definierten Radius.
Eigentlich braucht man die Rundung nicht, ich fand das nur optisch ansprechender.
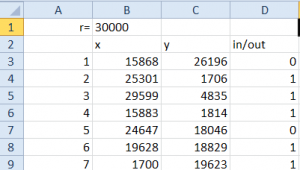
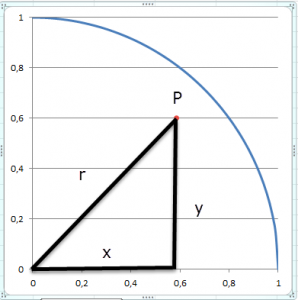
Jetzt kommt der gute alte Pythagoras ins Spiel, mit seinem Satz (Das Hypotenusen Quadrat in einem Rechtwinkligen Dreieck ist gleich der Summe beider Katheten Quadraten oder auch a² + b² = c²) kann man feststellen ob der Punkt mit den Koordinaten x und y innerhalb oder außerhalb des Kreises mit Radius rK liegt, und dies Geschieht in Spalte D mit der Formel:
=WENN(WURZEL(B3^2+C3^2)>$B$1;0;1)
Also wenn rP größer als rK ist, dann setzt Excel eine 0 und wenn nicht eine 1, damit lassen wir uns auf simpelste binäre Art und Weise anzeigen ob der Punkt innerhalb oder außerhalb des Kreises liegt
rP² = xp² + yp²
Jetzt müssen wir nur noch unsere 1er und 0er addieren, und durch ihre Anzahl teilen um ¼ Pi zu erhalten und mit 4 multiplizieren um Pi zu erhalten.
Genau das ist wieder einmal ein Paradebeispiel dafür wie viele unterschiedliche Möglichkeiten es in Excel gibt um ans Ziel zu kommen:
=ZÄHLENWENN(D:D;1)/ANZAHL(D:D)*4
oder
=SUMME(D:D)/ANZAHL(D:D)*4
oder
=MITTELWERT(D:D)*4
Und siehe da, wir haben einen Näherungswert für Pi.
Durch Drücken der Taste F9 könnt ihr sämtliche Formeln mit ZUFALLSZAHL() neu berechnen lassen.
Natürlich wird dieser Wert ‚besser‘ je mehr Punkte man Excel generieren lässt, wenn man die Zufallszahl-Formeln bis auf mindestens 50.000 runter zieht, erhält man schon relativ genaue Werte, die fast immer erst in der Tausendstelstelle abweichen. Je mehr Schüsse, umso besser die Annäherung, wie uns das Gesetz der großen Zahlen zeigt.
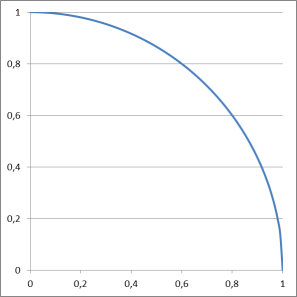
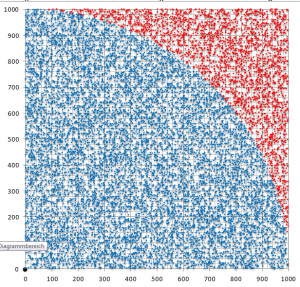
Wer die Sache jetzt gerne noch visualisieren möchte, der kann mit Excel eine Grafik ähnlich dieser hier generieren, und die Zufallsergebnisse auch noch optisch darstellen:
Um eine solche Grafik zu erstellen habe ich die Koordinaten der Punkte die in den Spalten B und C per Zufall erstellt wurden auf 4 Spalten verteilt, 2 Spalten für die X- und Y-Koordinate der blauen Punkte innerhalb des Kreises, und 2 Spalten für die Koordinaten der roten Punkte außerhalb des Kreises. Dazu bemühen wir wieder die altbekannte WENN Abfrage:
X Koordinate blaue Punkte: =WENN(D3;B3;0)
Y Koordinate blaue Punkte: =WENN(D3;C3;0)
X Koordinate rote Punkte: =WENN(D3;0;B3)
Y Koordinate rote Punkte: =WENN(D3;0;C3)
Besonders an dieser Art der WENN Abfrage ist, dass man wenn man eine Spalte oder einen Bereich abfragt, in dem nur 1 und 0 stehen, oder WAHR und FALSCH, man sich die Operanden sparen kann. Ein „WENN(A1=1;x;y)“ kann man auch als „WENN(A1;x;y)“ formulieren.
Mit diesen Daten kann man nun in einem Punkte-Diagramm (Punkte(X|Y)) zwei verschiedenfarbige Punktgruppen anzeigen lassen.
Ihr könnt eine Beispieldatei hier herunterladen, beachtet jedoch, dass es notwendig ist die Formeln weiter runter zu ziehen, um brauchbare Ergebnisse zu erhalten.
Ich heiße Martin Fuchs und arbeite für Barclaycard Deutschland in Hamburg. In meiner Funktion als Analyst, Controller und Planer ist Excel seit 2001 mein stetiger Begleiter im Beruf. Ich hatte das Glück eine hervorragende MS-Office Grundschulung im Zuge meiner Ausbildung zum IT-Kaufmann erhalten zu haben, und habe stets versucht mein Spektrum autodidaktisch und mit Hilfe von Seiten wie diesem tollen Blog hier zu erweitern.

P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.







Hallo Martin,
… Montag gab es leider kein neues Thema!
Hast Du Urlaub oder erwartet uns morgen ein „riesen“ Artikel“?
Schönen Sonntag noch
Michael
Hallo Michael,
weder Urlaub noch ein kommender „riesen“ Artikel sind der Grund dafür. Ich werde auf absehbare Zeit die Artikel nur noch 14tägig veröffentlichen. Und zwar nicht deshalb, weil ich etwa keine Lust mehr hätte oder mir die Ideen ausgegangen wären. Sondern weil ein Teil meiner verfügbaren Zeit gerade in ein anderes (Excel-)Projekt läuft 🙂
Schöne Grüße,
Martin